7.6. Serialization#
Import Python libraries
from __future__ import annotations
import json
import logging
import math
import os
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from IPython.display import Markdown
from scipy.interpolate import RegularGridInterpolator, griddata
from tqdm.auto import tqdm
from polarimetry import formulate_polarimetry
from polarimetry.data import (
create_data_transformer,
generate_meshgrid_sample,
generate_phasespace_sample,
)
from polarimetry.io import (
export_polarimetry_field,
import_polarimetry_field,
mute_jax_warnings,
perform_cached_doit,
perform_cached_lambdify,
)
from polarimetry.lhcb import load_model_builder, load_model_parameters
from polarimetry.lhcb.particle import load_particles
from polarimetry.plot import use_mpl_latex_fonts
logging.getLogger().setLevel(logging.ERROR)
mute_jax_warnings()
model_choice = "Default amplitude model"
model_file = "../../data/model-definitions.yaml"
particles = load_particles("../../data/particle-definitions.yaml")
amplitude_builder = load_model_builder(model_file, particles, model_choice)
imported_parameter_values = load_model_parameters(
model_file, amplitude_builder.decay, model_choice, particles
)
reference_subsystem = 1
model = amplitude_builder.formulate(reference_subsystem)
model.parameter_defaults.update(imported_parameter_values)
NO_TQDM = "EXECUTE_NB" in os.environ
if NO_TQDM:
logging.getLogger().setLevel(logging.ERROR)
Formulate expressions and lambdify
polarimetry_exprs = formulate_polarimetry(amplitude_builder, reference_subsystem)
unfolded_exprs = [
perform_cached_doit(expr.doit().xreplace(model.amplitudes))
for expr in tqdm(
[model.full_expression, *polarimetry_exprs], disable=NO_TQDM, leave=False
)
]
actual_funcs = [
perform_cached_lambdify(expr.xreplace(model.parameter_defaults), backend="jax")
for expr in tqdm(
unfolded_exprs, leave=False, desc="Lambdifying", disable=NO_TQDM
)
]
7.6.1. File size checks#
Export do different file formats
alpha_x_func = actual_funcs[1]
alpha_x = alpha_x_func(grid_sample).real
df = pd.DataFrame(alpha_x, index=X[0], columns=Y[:, 0])
os.makedirs("export", exist_ok=True)
df.to_json("export/alpha-x-pandas.json")
df.to_json("export/alpha-x-pandas-json.zip", compression={"method": "zip"})
df.to_csv("export/alpha-x-pandas.csv")
df_dict = df.to_dict()
filtered_df_dict = {
x: {y: v for y, v in row.items() if not math.isnan(v)}
for x, row in df_dict.items()
}
with open("export/alpha-x-python.json", "w") as f:
json.dump(filtered_df_dict, f)
json_dict = dict(
x=X[0].tolist(),
y=Y[:, 0].tolist(),
z=alpha_x.tolist(),
)
with open("export/alpha-x-arrays.json", "w") as f:
json.dump(json_dict, f, separators=(",", ":"))
File sizes for 100x100 grid:
File type |
Size |
|---|---|
141 kB |
|
311 kB |
|
260 kB |
|
51 kB |
|
129 kB |
7.6.2. Export polarimetry grids#
Decided to use the alpha-x-arrays.json format. It can be exported with export_polarimetry_field().
os.makedirs("export", exist_ok=True)
filename = "export/polarimetry-model-0.json"
export_polarimetry_field(
sigma1=X[0],
sigma2=Y[:, 0],
intensity=actual_funcs[0](grid_sample).real,
alpha_x=actual_funcs[1](grid_sample).real,
alpha_y=actual_funcs[2](grid_sample).real,
alpha_z=actual_funcs[3](grid_sample).real,
filename=filename,
metadata={"model description": model_choice},
)
Polarimetry grid can be downloaded here: export/polarimetry-model-0.json (540 kB).
7.6.3. Import and interpolate#
The arrays in the exported JSON files can be used to create a RegularGridInterpolator for the intensity and for each components of \(\vec\alpha\).
field_definition = import_polarimetry_field("export/polarimetry-model-0.json")
imported_sigma1 = field_definition["m^2_Kpi"]
imported_sigma2 = field_definition["m^2_pK"]
imported_arrays = (
field_definition["intensity"],
field_definition["alpha_x"],
field_definition["alpha_y"],
field_definition["alpha_z"],
)
interpolated_funcs = [
RegularGridInterpolator(
points=(
np.array(imported_sigma1),
np.array(imported_sigma2),
),
values=np.array(z).transpose(),
method="linear",
)
for z in imported_arrays
]
This is a function that can compute an interpolated value of each of these observables for a random point on the Dalitz plane.
interpolated_funcs[1]([0.8, 3.6])
array([0.18379986])
As opposed to SciPy’s deprecated interp2d, RegularGridInterpolator is already in vectorized form, so there is no need to vectorize it.
n_points = 100_000
mini_sample = generate_phasespace_sample(model.decay, n_points, seed=0)
mini_sample = transformer(mini_sample)
x = mini_sample["sigma1"]
y = mini_sample["sigma2"]
z_interpolated = [func((x, y)) for func in tqdm(interpolated_funcs, disable=NO_TQDM)]
z_interpolated[0]
array([2165.82154945, 5481.04128781, 6254.96174147, ..., 1369.40657535,
4456.44114915, 7197.97782088])
Show code cell source
use_mpl_latex_fonts()
plt.rc("font", size=18)
fig, axes = plt.subplots(
dpi=200,
figsize=(15, 11.5),
gridspec_kw={"width_ratios": [1, 1, 1, 1.2]},
ncols=4,
nrows=3,
sharex=True,
sharey=True,
)
plt.subplots_adjust(hspace=0.1, wspace=0.03)
fig.suptitle("Comparison interpolated and actual values", y=0.94)
points = np.transpose([x, y])
for i in tqdm(range(4), disable=NO_TQDM, leave=False):
if i == 0:
title = "$I$"
cmap = plt.cm.viridis
clim = None
else:
title = Rf"$\alpha_{'xyz'[i-1]}$"
cmap = plt.cm.coolwarm
clim = (-1, +1)
axes[0, i].set_title(title, y=1.03)
z_actual = actual_funcs[i](mini_sample)
z_diff = 100 * ((z_interpolated[i] - z_actual) / z_actual).real
Z_interpolated = griddata(points, z_interpolated[i], (X, Y))
Z_diff = griddata(points, z_diff, (X, Y))
mesh = (
axes[0, i].pcolormesh(X, Y, actual_funcs[i](grid_sample).real, cmap=cmap),
axes[1, i].pcolormesh(X, Y, Z_interpolated, cmap=cmap),
axes[2, i].pcolormesh(X, Y, Z_diff, clim=(-100, +100), cmap=plt.cm.coolwarm),
)
if i != 0:
mesh[0].set_clim(-1, +1)
mesh[1].set_clim(-1, +1)
if i == 3:
c_bar = [fig.colorbar(mesh[j], ax=axes[j, i], pad=0.015) for j in range(3)]
c_bar[0].ax.set_ylabel("Original distribution", labelpad=3)
c_bar[1].ax.set_ylabel("Interpolated distribution", labelpad=3)
c_bar[2].ax.set_ylabel("Difference", labelpad=-20)
for c in c_bar[:-1]:
c.ax.set_yticks([-1, 0, +1])
c.ax.set_yticklabels(["$-1$", "$0$", "$+1$"])
c_bar[-1].ax.set_yticks([-100, 0, +100])
c_bar[-1].ax.set_yticklabels([R"$-100\%$", R"$0\%$", R"$+100\%$"])
axes[0, i].text(
x=0.96,
y=0.83,
s=f"grid size:\n{resolution}x{resolution}",
fontsize=16,
horizontalalignment="right",
transform=axes[0, i].transAxes,
)
axes[1, i].text(
x=0.96,
y=0.83,
s=f"phsp size:\n{n_points:,}",
fontsize=16,
horizontalalignment="right",
transform=axes[1, i].transAxes,
)
plt.show()
plt.close(fig)
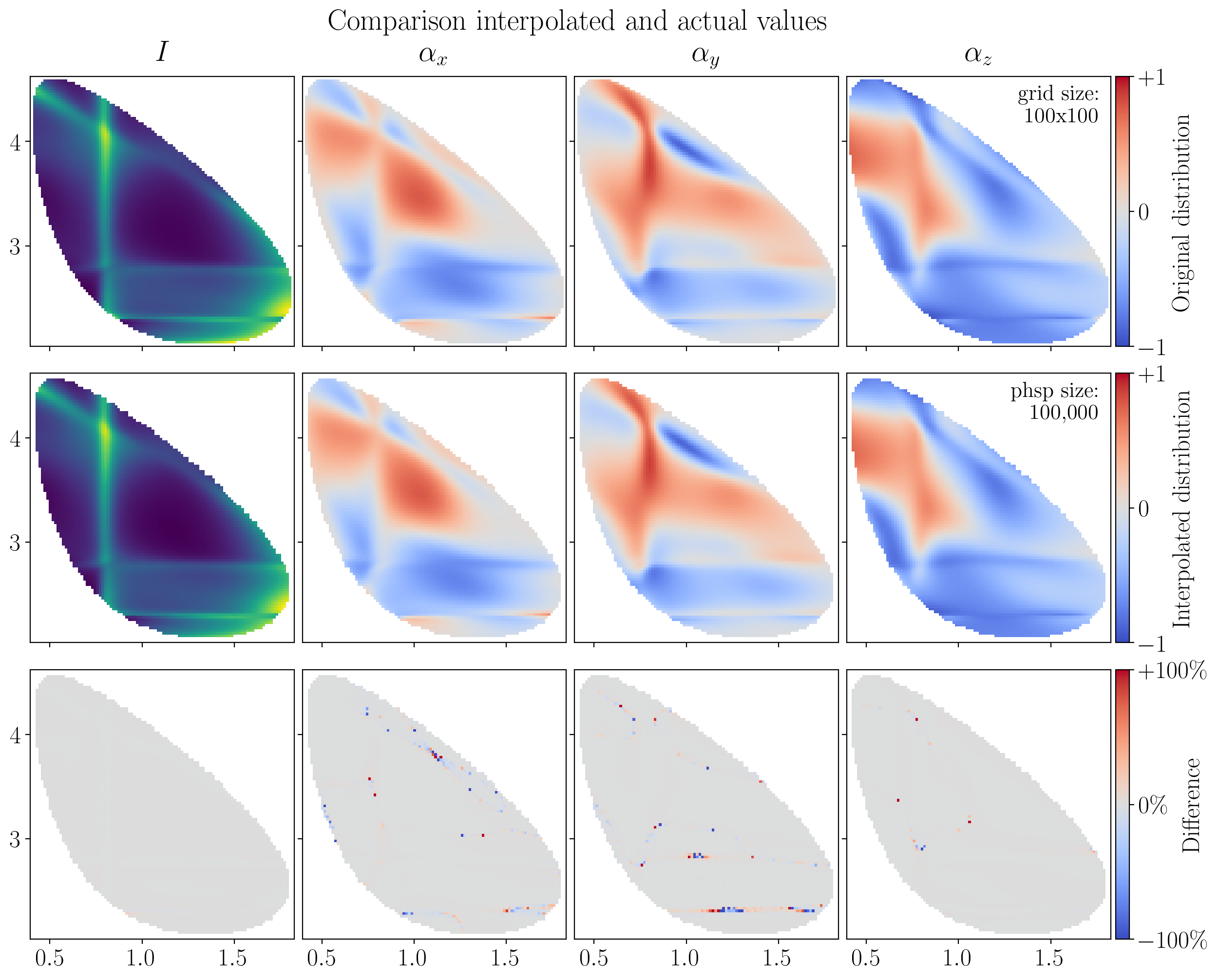
Note
The interpolated values over this phase space sample have been visualized by interpolating again over a meshgrid with scipy.interpolate.griddata.
Tip
Determination of polarization shows how this interpolation method can be used to determine the polarization \(\vec{P}\) from a given intensity distribution.
