7.7. Amplitude model with LS-couplings

Import python libraries Hide code cell content

from __future__ import annotations

import logging
import os

import jax
import jax.numpy as jnp
import matplotlib.pyplot as plt
import sympy as sp
from IPython.display import Latex
from sympy.core.symbol import Str
from tensorwaves.interface import Function
from tqdm.auto import tqdm

from polarimetry.amplitude import (
    AmplitudeModel,
    get_indexed_base,
    simplify_latex_rendering,
)
from polarimetry.data import (
    create_data_transformer,
    generate_meshgrid_sample,
    generate_phasespace_sample,
)
from polarimetry.decay import Particle
from polarimetry.function import integrate_intensity, sub_intensity
from polarimetry.io import (
    as_latex,
    display_latex,
    mute_jax_warnings,
    perform_cached_doit,
    perform_cached_lambdify,
)
from polarimetry.lhcb import (
    get_conversion_factor_ls,
    load_model_builder,
    load_model_parameters,
)
from polarimetry.lhcb.particle import load_particles
from polarimetry.plot import use_mpl_latex_fonts

mute_jax_warnings()
simplify_latex_rendering()
MODEL_FILE = "../../data/model-definitions.yaml"
PARTICLES = load_particles("../../data/particle-definitions.yaml")

NO_TQDM = "EXECUTE_NB" in os.environ
if NO_TQDM:
    logging.getLogger().setLevel(logging.ERROR)
    logging.getLogger("polarimetry.io").setLevel(logging.ERROR)
    logging.getLogger("tensorwaves.data").setLevel(logging.ERROR)

7.7.1. Model inspection

Show code cell source Hide code cell source

def formulate_model(title: str) -> AmplitudeModel:
    builder = load_model_builder(MODEL_FILE, PARTICLES, title)
    imported_parameters = load_model_parameters(
        MODEL_FILE, builder.decay, title, PARTICLES
    )
    model = builder.formulate()
    model.parameter_defaults.update(imported_parameters)
    return model


def simplify_notation(expr: sp.Expr) -> sp.Expr:
    def substitute_node(node):
        if isinstance(node, sp.Indexed) and node.indices[2:] == (0, 0):
            return sp.Indexed(node.base, *node.indices[:2])
        return node

    for node in sp.preorder_traversal(expr):
        new_node = substitute_node(node)
        expr = expr.xreplace({node: new_node})
    return expr


LS_MODEL = formulate_model("Alternative amplitude model obtained using LS couplings")
simplify_notation(LS_MODEL.intensity.args[0].args[0].args[0].cleanup())

\[\displaystyle \sum_{\lambda_0^{\prime}=-1/2}^{1/2} \sum_{\lambda_1^{\prime}=-1/2}^{1/2}{A^{1}_{\lambda_0^{\prime}, \lambda_1^{\prime}} d^{\frac{1}{2}}_{\lambda_1^{\prime},\lambda_{1}}\left(\zeta^1_{1(1)}\right) d^{\frac{1}{2}}_{\lambda_{0},\lambda_0^{\prime}}\left(\zeta^0_{1(1)}\right) + A^{2}_{\lambda_0^{\prime}, \lambda_1^{\prime}} d^{\frac{1}{2}}_{\lambda_1^{\prime},\lambda_{1}}\left(\zeta^1_{2(1)}\right) d^{\frac{1}{2}}_{\lambda_{0},\lambda_0^{\prime}}\left(\zeta^0_{2(1)}\right) + A^{3}_{\lambda_0^{\prime}, \lambda_1^{\prime}} d^{\frac{1}{2}}_{\lambda_1^{\prime},\lambda_{1}}\left(\zeta^1_{3(1)}\right) d^{\frac{1}{2}}_{\lambda_{0},\lambda_0^{\prime}}\left(\zeta^0_{3(1)}\right)}\]

Show code cell source Hide code cell source

display_latex({simplify_notation(k): v for k, v in LS_MODEL.amplitudes.items()})

\[\begin{split}\displaystyle \begin{array}{rcl} A^{1}_{- \frac{1}{2}, - \frac{1}{2}} &=& \sum_{\lambda_{R}=-1}^{1}{- \frac{\sqrt{10} \delta_{- \frac{1}{2}, \lambda_{R} + \frac{1}{2}} \mathcal{R}\left(\sigma_{1}\right) C^{\frac{3}{2},\lambda_{R} + \frac{1}{2}}_{1,\lambda_{R},\frac{1}{2},\frac{1}{2}} C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{2,0,\frac{3}{2},\lambda_{R} + \frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(892), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{K(892), 0, 0} d^{1}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=-1}^{1}{- \frac{\sqrt{2} \delta_{- \frac{1}{2}, \lambda_{R} + \frac{1}{2}} \mathcal{R}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{0,0,\frac{1}{2},\lambda_{R} + \frac{1}{2}} C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{1,\lambda_{R},\frac{1}{2},\frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(892), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(892), 0, 0} d^{1}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=0}{- \frac{\sqrt{2} \delta_{- \frac{1}{2}, \lambda_{R} + \frac{1}{2}} \mathcal{R}_\mathrm{Bugg}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{0,0,\frac{1}{2},\lambda_{R} + \frac{1}{2}} C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{0,\lambda_{R},\frac{1}{2},\frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(1430), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(1430), 0, 0} d^{0}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=0}{- \frac{\sqrt{2} \delta_{- \frac{1}{2}, \lambda_{R} + \frac{1}{2}} \mathcal{R}_\mathrm{Bugg}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{0,0,\frac{1}{2},\lambda_{R} + \frac{1}{2}} C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{0,\lambda_{R},\frac{1}{2},\frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(700), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(700), 0, 0} d^{0}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=-1}^{1}{- \frac{\sqrt{6} \delta_{- \frac{1}{2}, \lambda_{R} + \frac{1}{2}} \mathcal{R}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{1,0,\frac{1}{2},\lambda_{R} + \frac{1}{2}} C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{1,\lambda_{R},\frac{1}{2},\frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(892), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(892), 0, 0} d^{1}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=-1}^{1}{- \frac{\sqrt{6} \delta_{- \frac{1}{2}, \lambda_{R} + \frac{1}{2}} \mathcal{R}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{1,0,\frac{3}{2},\lambda_{R} + \frac{1}{2}} C^{\frac{3}{2},\lambda_{R} + \frac{1}{2}}_{1,\lambda_{R},\frac{1}{2},\frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(892), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{K(892), 0, 0} d^{1}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=0}{- \frac{\sqrt{6} \delta_{- \frac{1}{2}, \lambda_{R} + \frac{1}{2}} \mathcal{R}_\mathrm{Bugg}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{0,\lambda_{R},\frac{1}{2},\frac{1}{2}} C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{1,0,\frac{1}{2},\lambda_{R} + \frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(1430), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(1430), 0, 0} d^{0}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=0}{- \frac{\sqrt{6} \delta_{- \frac{1}{2}, \lambda_{R} + \frac{1}{2}} \mathcal{R}_\mathrm{Bugg}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{0,\lambda_{R},\frac{1}{2},\frac{1}{2}} C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{1,0,\frac{1}{2},\lambda_{R} + \frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(700), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(700), 0, 0} d^{0}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} \\ A^{2}_{- \frac{1}{2}, - \frac{1}{2}} &=& \sum_{\lambda_{R}=-3/2}^{3/2}{- \frac{\sqrt{10} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{2,0,\frac{3}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{L(1520), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{L(1520), 0, - \frac{1}{2}} d^{\frac{3}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{- \frac{\sqrt{10} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{2,0,\frac{3}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{L(1690), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{L(1690), 0, - \frac{1}{2}} d^{\frac{3}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{- \frac{\sqrt{2} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{0,0,\frac{1}{2},\lambda_{R}} C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{L(1600), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1600), 0, - \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{- \frac{\sqrt{2} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{0,0,\frac{1}{2},\lambda_{R}} C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{L(1670), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1670), 0, - \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{- \frac{\sqrt{2} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{0,0,\frac{1}{2},\lambda_{R}} C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{L(2000), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(2000), 0, - \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{- \frac{\sqrt{6} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{3}{2},\lambda_{R}} C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{L(1520), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{L(1520), 0, - \frac{1}{2}} d^{\frac{3}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{- \frac{\sqrt{6} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{1}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{L(1600), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1600), 0, - \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{- \frac{\sqrt{6} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{1}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{L(1670), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1670), 0, - \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{- \frac{\sqrt{6} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{3}{2},\lambda_{R}} C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{L(1690), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{L(1690), 0, - \frac{1}{2}} d^{\frac{3}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{- \frac{\sqrt{6} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{1}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{L(2000), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(2000), 0, - \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{- \frac{\sqrt{2} \delta_{- \frac{1}{2} \lambda_{R}} F_{0}\left(R_{\Lambda_c} q_{m_{0},m_{2}}\left(\sigma_{2}\right)\right) C^{\frac{1}{2},\lambda_{R}}_{0,0,\frac{1}{2},\lambda_{R}} C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} \mathcal{R}_\mathrm{Flatté}\left(\sigma_{2}\right) \mathcal{H}^\mathrm{LS,production}_{L(1405), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1405), 0, - \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2 F_{0}\left(R_{\Lambda_c} q_{m_{0},m_{2}}\left(m_{L(1405)}^{2}\right)\right)}} + \sum_{\lambda_{R}=-1/2}^{1/2}{- \frac{\sqrt{6} \delta_{- \frac{1}{2} \lambda_{R}} F_{1}\left(R_{\Lambda_c} q_{m_{0},m_{2}}\left(\sigma_{2}\right)\right) C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{1}{2},\lambda_{R}} \mathcal{R}_\mathrm{Flatté}\left(\sigma_{2}\right) \mathcal{H}^\mathrm{LS,production}_{L(1405), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1405), 0, - \frac{1}{2}} q_{m_{0},m_{2}}\left(\sigma_{2}\right) d^{\frac{1}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2 F_{1}\left(R_{\Lambda_c} q_{m_{0},m_{2}}\left(m_{L(1405)}^{2}\right)\right) q_{m_{0},m_{2}}\left(m_{L(1405)}^{2}\right)}} \\ A^{3}_{- \frac{1}{2}, - \frac{1}{2}} &=& \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{10} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{2,0,\frac{3}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{D(1232), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1232), - \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{12}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{10} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{2,0,\frac{3}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{D(1600), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1600), - \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{12}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{10} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{2,0,\frac{3}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{D(1700), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1700), - \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{12}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{6} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{3}{2},\lambda_{R}} C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{D(1232), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1232), - \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{12}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{6} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{3}{2},\lambda_{R}} C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{D(1600), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1600), - \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{12}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{6} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{3}{2},\lambda_{R}} C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{D(1700), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1700), - \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{12}\right)}{2}} \\ A^{1}_{- \frac{1}{2}, \frac{1}{2}} &=& \sum_{\lambda_{R}=-1}^{1}{\frac{\sqrt{10} \delta_{- \frac{1}{2}, \lambda_{R} - \frac{1}{2}} \mathcal{R}\left(\sigma_{1}\right) C^{\frac{3}{2},\lambda_{R} - \frac{1}{2}}_{1,\lambda_{R},\frac{1}{2},- \frac{1}{2}} C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{2,0,\frac{3}{2},\lambda_{R} - \frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(892), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{K(892), 0, 0} d^{1}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=-1}^{1}{\frac{\sqrt{2} \delta_{- \frac{1}{2}, \lambda_{R} - \frac{1}{2}} \mathcal{R}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{0,0,\frac{1}{2},\lambda_{R} - \frac{1}{2}} C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{1,\lambda_{R},\frac{1}{2},- \frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(892), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(892), 0, 0} d^{1}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=0}{\frac{\sqrt{2} \delta_{- \frac{1}{2}, \lambda_{R} - \frac{1}{2}} \mathcal{R}_\mathrm{Bugg}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{0,0,\frac{1}{2},\lambda_{R} - \frac{1}{2}} C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{0,\lambda_{R},\frac{1}{2},- \frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(1430), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(1430), 0, 0} d^{0}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=0}{\frac{\sqrt{2} \delta_{- \frac{1}{2}, \lambda_{R} - \frac{1}{2}} \mathcal{R}_\mathrm{Bugg}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{0,0,\frac{1}{2},\lambda_{R} - \frac{1}{2}} C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{0,\lambda_{R},\frac{1}{2},- \frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(700), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(700), 0, 0} d^{0}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=-1}^{1}{\frac{\sqrt{6} \delta_{- \frac{1}{2}, \lambda_{R} - \frac{1}{2}} \mathcal{R}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{1,0,\frac{1}{2},\lambda_{R} - \frac{1}{2}} C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{1,\lambda_{R},\frac{1}{2},- \frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(892), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(892), 0, 0} d^{1}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=-1}^{1}{\frac{\sqrt{6} \delta_{- \frac{1}{2}, \lambda_{R} - \frac{1}{2}} \mathcal{R}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{1,0,\frac{3}{2},\lambda_{R} - \frac{1}{2}} C^{\frac{3}{2},\lambda_{R} - \frac{1}{2}}_{1,\lambda_{R},\frac{1}{2},- \frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(892), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{K(892), 0, 0} d^{1}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=0}{\frac{\sqrt{6} \delta_{- \frac{1}{2}, \lambda_{R} - \frac{1}{2}} \mathcal{R}_\mathrm{Bugg}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{0,\lambda_{R},\frac{1}{2},- \frac{1}{2}} C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{1,0,\frac{1}{2},\lambda_{R} - \frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(1430), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(1430), 0, 0} d^{0}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=0}{\frac{\sqrt{6} \delta_{- \frac{1}{2}, \lambda_{R} - \frac{1}{2}} \mathcal{R}_\mathrm{Bugg}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{0,\lambda_{R},\frac{1}{2},- \frac{1}{2}} C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{1,0,\frac{1}{2},\lambda_{R} - \frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(700), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(700), 0, 0} d^{0}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} \\ A^{2}_{- \frac{1}{2}, \frac{1}{2}} &=& \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{10} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{2,0,\frac{3}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{L(1520), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{L(1520), 0, \frac{1}{2}} d^{\frac{3}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{10} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{2,0,\frac{3}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{L(1690), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{L(1690), 0, \frac{1}{2}} d^{\frac{3}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{\frac{\sqrt{2} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{0,0,\frac{1}{2},\lambda_{R}} C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{L(1600), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1600), 0, \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{\frac{\sqrt{2} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{0,0,\frac{1}{2},\lambda_{R}} C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{L(1670), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1670), 0, \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{\frac{\sqrt{2} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{0,0,\frac{1}{2},\lambda_{R}} C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{L(2000), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(2000), 0, \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{6} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{3}{2},\lambda_{R}} C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{L(1520), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{L(1520), 0, \frac{1}{2}} d^{\frac{3}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{\frac{\sqrt{6} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{1}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{L(1600), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1600), 0, \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{\frac{\sqrt{6} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{1}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{L(1670), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1670), 0, \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{6} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{3}{2},\lambda_{R}} C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{L(1690), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{L(1690), 0, \frac{1}{2}} d^{\frac{3}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{\frac{\sqrt{6} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{1}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{L(2000), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(2000), 0, \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{\frac{\sqrt{2} \delta_{- \frac{1}{2} \lambda_{R}} F_{0}\left(R_{\Lambda_c} q_{m_{0},m_{2}}\left(\sigma_{2}\right)\right) C^{\frac{1}{2},\lambda_{R}}_{0,0,\frac{1}{2},\lambda_{R}} C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} \mathcal{R}_\mathrm{Flatté}\left(\sigma_{2}\right) \mathcal{H}^\mathrm{LS,production}_{L(1405), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1405), 0, \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2 F_{0}\left(R_{\Lambda_c} q_{m_{0},m_{2}}\left(m_{L(1405)}^{2}\right)\right)}} + \sum_{\lambda_{R}=-1/2}^{1/2}{\frac{\sqrt{6} \delta_{- \frac{1}{2} \lambda_{R}} F_{1}\left(R_{\Lambda_c} q_{m_{0},m_{2}}\left(\sigma_{2}\right)\right) C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{1}{2},\lambda_{R}} \mathcal{R}_\mathrm{Flatté}\left(\sigma_{2}\right) \mathcal{H}^\mathrm{LS,production}_{L(1405), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1405), 0, \frac{1}{2}} q_{m_{0},m_{2}}\left(\sigma_{2}\right) d^{\frac{1}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2 F_{1}\left(R_{\Lambda_c} q_{m_{0},m_{2}}\left(m_{L(1405)}^{2}\right)\right) q_{m_{0},m_{2}}\left(m_{L(1405)}^{2}\right)}} \\ A^{3}_{- \frac{1}{2}, \frac{1}{2}} &=& \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{10} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{2,0,\frac{3}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{D(1232), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1232), \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{12}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{10} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{2,0,\frac{3}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{D(1600), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1600), \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{12}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{10} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{2,0,\frac{3}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{D(1700), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1700), \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{12}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{6} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{3}{2},\lambda_{R}} C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{D(1232), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1232), \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{12}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{6} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{3}{2},\lambda_{R}} C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{D(1600), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1600), \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{12}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{6} \delta_{- \frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{3}{2},\lambda_{R}} C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{D(1700), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1700), \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{12}\right)}{2}} \\ A^{1}_{\frac{1}{2}, - \frac{1}{2}} &=& \sum_{\lambda_{R}=-1}^{1}{- \frac{\sqrt{10} \delta_{\frac{1}{2}, \lambda_{R} + \frac{1}{2}} \mathcal{R}\left(\sigma_{1}\right) C^{\frac{3}{2},\lambda_{R} + \frac{1}{2}}_{1,\lambda_{R},\frac{1}{2},\frac{1}{2}} C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{2,0,\frac{3}{2},\lambda_{R} + \frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(892), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{K(892), 0, 0} d^{1}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=-1}^{1}{- \frac{\sqrt{2} \delta_{\frac{1}{2}, \lambda_{R} + \frac{1}{2}} \mathcal{R}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{0,0,\frac{1}{2},\lambda_{R} + \frac{1}{2}} C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{1,\lambda_{R},\frac{1}{2},\frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(892), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(892), 0, 0} d^{1}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=0}{- \frac{\sqrt{2} \delta_{\frac{1}{2}, \lambda_{R} + \frac{1}{2}} \mathcal{R}_\mathrm{Bugg}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{0,0,\frac{1}{2},\lambda_{R} + \frac{1}{2}} C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{0,\lambda_{R},\frac{1}{2},\frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(1430), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(1430), 0, 0} d^{0}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=0}{- \frac{\sqrt{2} \delta_{\frac{1}{2}, \lambda_{R} + \frac{1}{2}} \mathcal{R}_\mathrm{Bugg}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{0,0,\frac{1}{2},\lambda_{R} + \frac{1}{2}} C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{0,\lambda_{R},\frac{1}{2},\frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(700), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(700), 0, 0} d^{0}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=-1}^{1}{- \frac{\sqrt{6} \delta_{\frac{1}{2}, \lambda_{R} + \frac{1}{2}} \mathcal{R}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{1,0,\frac{1}{2},\lambda_{R} + \frac{1}{2}} C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{1,\lambda_{R},\frac{1}{2},\frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(892), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(892), 0, 0} d^{1}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=-1}^{1}{- \frac{\sqrt{6} \delta_{\frac{1}{2}, \lambda_{R} + \frac{1}{2}} \mathcal{R}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{1,0,\frac{3}{2},\lambda_{R} + \frac{1}{2}} C^{\frac{3}{2},\lambda_{R} + \frac{1}{2}}_{1,\lambda_{R},\frac{1}{2},\frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(892), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{K(892), 0, 0} d^{1}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=0}{- \frac{\sqrt{6} \delta_{\frac{1}{2}, \lambda_{R} + \frac{1}{2}} \mathcal{R}_\mathrm{Bugg}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{0,\lambda_{R},\frac{1}{2},\frac{1}{2}} C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{1,0,\frac{1}{2},\lambda_{R} + \frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(1430), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(1430), 0, 0} d^{0}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=0}{- \frac{\sqrt{6} \delta_{\frac{1}{2}, \lambda_{R} + \frac{1}{2}} \mathcal{R}_\mathrm{Bugg}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{0,\lambda_{R},\frac{1}{2},\frac{1}{2}} C^{\frac{1}{2},\lambda_{R} + \frac{1}{2}}_{1,0,\frac{1}{2},\lambda_{R} + \frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(700), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(700), 0, 0} d^{0}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} \\ A^{2}_{\frac{1}{2}, - \frac{1}{2}} &=& \sum_{\lambda_{R}=-3/2}^{3/2}{- \frac{\sqrt{10} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{2,0,\frac{3}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{L(1520), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{L(1520), 0, - \frac{1}{2}} d^{\frac{3}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{- \frac{\sqrt{10} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{2,0,\frac{3}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{L(1690), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{L(1690), 0, - \frac{1}{2}} d^{\frac{3}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{- \frac{\sqrt{2} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{0,0,\frac{1}{2},\lambda_{R}} C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{L(1600), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1600), 0, - \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{- \frac{\sqrt{2} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{0,0,\frac{1}{2},\lambda_{R}} C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{L(1670), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1670), 0, - \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{- \frac{\sqrt{2} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{0,0,\frac{1}{2},\lambda_{R}} C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{L(2000), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(2000), 0, - \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{- \frac{\sqrt{6} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{3}{2},\lambda_{R}} C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{L(1520), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{L(1520), 0, - \frac{1}{2}} d^{\frac{3}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{- \frac{\sqrt{6} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{1}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{L(1600), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1600), 0, - \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{- \frac{\sqrt{6} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{1}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{L(1670), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1670), 0, - \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{- \frac{\sqrt{6} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{3}{2},\lambda_{R}} C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{L(1690), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{L(1690), 0, - \frac{1}{2}} d^{\frac{3}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{- \frac{\sqrt{6} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{1}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{L(2000), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(2000), 0, - \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{- \frac{\sqrt{2} \delta_{\frac{1}{2} \lambda_{R}} F_{0}\left(R_{\Lambda_c} q_{m_{0},m_{2}}\left(\sigma_{2}\right)\right) C^{\frac{1}{2},\lambda_{R}}_{0,0,\frac{1}{2},\lambda_{R}} C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} \mathcal{R}_\mathrm{Flatté}\left(\sigma_{2}\right) \mathcal{H}^\mathrm{LS,production}_{L(1405), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1405), 0, - \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2 F_{0}\left(R_{\Lambda_c} q_{m_{0},m_{2}}\left(m_{L(1405)}^{2}\right)\right)}} + \sum_{\lambda_{R}=-1/2}^{1/2}{- \frac{\sqrt{6} \delta_{\frac{1}{2} \lambda_{R}} F_{1}\left(R_{\Lambda_c} q_{m_{0},m_{2}}\left(\sigma_{2}\right)\right) C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{1}{2},\lambda_{R}} \mathcal{R}_\mathrm{Flatté}\left(\sigma_{2}\right) \mathcal{H}^\mathrm{LS,production}_{L(1405), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1405), 0, - \frac{1}{2}} q_{m_{0},m_{2}}\left(\sigma_{2}\right) d^{\frac{1}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{31}\right)}{2 F_{1}\left(R_{\Lambda_c} q_{m_{0},m_{2}}\left(m_{L(1405)}^{2}\right)\right) q_{m_{0},m_{2}}\left(m_{L(1405)}^{2}\right)}} \\ A^{3}_{\frac{1}{2}, - \frac{1}{2}} &=& \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{10} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{2,0,\frac{3}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{D(1232), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1232), - \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{12}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{10} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{2,0,\frac{3}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{D(1600), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1600), - \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{12}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{10} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{2,0,\frac{3}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{D(1700), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1700), - \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{12}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{6} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{3}{2},\lambda_{R}} C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{D(1232), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1232), - \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{12}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{6} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{3}{2},\lambda_{R}} C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{D(1600), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1600), - \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{12}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{6} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{3}{2},\lambda_{R}} C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{D(1700), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1700), - \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{12}\right)}{2}} \\ A^{1}_{\frac{1}{2}, \frac{1}{2}} &=& \sum_{\lambda_{R}=-1}^{1}{\frac{\sqrt{10} \delta_{\frac{1}{2}, \lambda_{R} - \frac{1}{2}} \mathcal{R}\left(\sigma_{1}\right) C^{\frac{3}{2},\lambda_{R} - \frac{1}{2}}_{1,\lambda_{R},\frac{1}{2},- \frac{1}{2}} C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{2,0,\frac{3}{2},\lambda_{R} - \frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(892), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{K(892), 0, 0} d^{1}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=-1}^{1}{\frac{\sqrt{2} \delta_{\frac{1}{2}, \lambda_{R} - \frac{1}{2}} \mathcal{R}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{0,0,\frac{1}{2},\lambda_{R} - \frac{1}{2}} C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{1,\lambda_{R},\frac{1}{2},- \frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(892), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(892), 0, 0} d^{1}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=0}{\frac{\sqrt{2} \delta_{\frac{1}{2}, \lambda_{R} - \frac{1}{2}} \mathcal{R}_\mathrm{Bugg}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{0,0,\frac{1}{2},\lambda_{R} - \frac{1}{2}} C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{0,\lambda_{R},\frac{1}{2},- \frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(1430), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(1430), 0, 0} d^{0}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=0}{\frac{\sqrt{2} \delta_{\frac{1}{2}, \lambda_{R} - \frac{1}{2}} \mathcal{R}_\mathrm{Bugg}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{0,0,\frac{1}{2},\lambda_{R} - \frac{1}{2}} C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{0,\lambda_{R},\frac{1}{2},- \frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(700), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(700), 0, 0} d^{0}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=-1}^{1}{\frac{\sqrt{6} \delta_{\frac{1}{2}, \lambda_{R} - \frac{1}{2}} \mathcal{R}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{1,0,\frac{1}{2},\lambda_{R} - \frac{1}{2}} C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{1,\lambda_{R},\frac{1}{2},- \frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(892), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(892), 0, 0} d^{1}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=-1}^{1}{\frac{\sqrt{6} \delta_{\frac{1}{2}, \lambda_{R} - \frac{1}{2}} \mathcal{R}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{1,0,\frac{3}{2},\lambda_{R} - \frac{1}{2}} C^{\frac{3}{2},\lambda_{R} - \frac{1}{2}}_{1,\lambda_{R},\frac{1}{2},- \frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(892), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{K(892), 0, 0} d^{1}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=0}{\frac{\sqrt{6} \delta_{\frac{1}{2}, \lambda_{R} - \frac{1}{2}} \mathcal{R}_\mathrm{Bugg}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{0,\lambda_{R},\frac{1}{2},- \frac{1}{2}} C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{1,0,\frac{1}{2},\lambda_{R} - \frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(1430), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(1430), 0, 0} d^{0}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} + \sum_{\lambda_{R}=0}{\frac{\sqrt{6} \delta_{\frac{1}{2}, \lambda_{R} - \frac{1}{2}} \mathcal{R}_\mathrm{Bugg}\left(\sigma_{1}\right) C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{0,\lambda_{R},\frac{1}{2},- \frac{1}{2}} C^{\frac{1}{2},\lambda_{R} - \frac{1}{2}}_{1,0,\frac{1}{2},\lambda_{R} - \frac{1}{2}} \mathcal{H}^\mathrm{LS,production}_{K(700), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{K(700), 0, 0} d^{0}_{\lambda_{R},0}\left(\theta_{23}\right)}{2}} \\ A^{2}_{\frac{1}{2}, \frac{1}{2}} &=& \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{10} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{2,0,\frac{3}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{L(1520), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{L(1520), 0, \frac{1}{2}} d^{\frac{3}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{10} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{2,0,\frac{3}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{L(1690), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{L(1690), 0, \frac{1}{2}} d^{\frac{3}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{\frac{\sqrt{2} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{0,0,\frac{1}{2},\lambda_{R}} C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{L(1600), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1600), 0, \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{\frac{\sqrt{2} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{0,0,\frac{1}{2},\lambda_{R}} C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{L(1670), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1670), 0, \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{\frac{\sqrt{2} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{0,0,\frac{1}{2},\lambda_{R}} C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{L(2000), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(2000), 0, \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{6} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{3}{2},\lambda_{R}} C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{L(1520), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{L(1520), 0, \frac{1}{2}} d^{\frac{3}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{\frac{\sqrt{6} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{1}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{L(1600), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1600), 0, \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{\frac{\sqrt{6} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{1}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{L(1670), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1670), 0, \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{6} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{3}{2},\lambda_{R}} C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{L(1690), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{L(1690), 0, \frac{1}{2}} d^{\frac{3}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{\frac{\sqrt{6} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{2}\right) C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{1}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{L(2000), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(2000), 0, \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2}} + \sum_{\lambda_{R}=-1/2}^{1/2}{\frac{\sqrt{2} \delta_{\frac{1}{2} \lambda_{R}} F_{0}\left(R_{\Lambda_c} q_{m_{0},m_{2}}\left(\sigma_{2}\right)\right) C^{\frac{1}{2},\lambda_{R}}_{0,0,\frac{1}{2},\lambda_{R}} C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} \mathcal{R}_\mathrm{Flatté}\left(\sigma_{2}\right) \mathcal{H}^\mathrm{LS,production}_{L(1405), 0, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1405), 0, \frac{1}{2}} d^{\frac{1}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2 F_{0}\left(R_{\Lambda_c} q_{m_{0},m_{2}}\left(m_{L(1405)}^{2}\right)\right)}} + \sum_{\lambda_{R}=-1/2}^{1/2}{\frac{\sqrt{6} \delta_{\frac{1}{2} \lambda_{R}} F_{1}\left(R_{\Lambda_c} q_{m_{0},m_{2}}\left(\sigma_{2}\right)\right) C^{\frac{1}{2},\lambda_{R}}_{\frac{1}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{1}{2},\lambda_{R}} \mathcal{R}_\mathrm{Flatté}\left(\sigma_{2}\right) \mathcal{H}^\mathrm{LS,production}_{L(1405), 1, \frac{1}{2}} \mathcal{H}^\mathrm{decay}_{L(1405), 0, \frac{1}{2}} q_{m_{0},m_{2}}\left(\sigma_{2}\right) d^{\frac{1}{2}}_{\lambda_{R},- \frac{1}{2}}\left(\theta_{31}\right)}{2 F_{1}\left(R_{\Lambda_c} q_{m_{0},m_{2}}\left(m_{L(1405)}^{2}\right)\right) q_{m_{0},m_{2}}\left(m_{L(1405)}^{2}\right)}} \\ A^{3}_{\frac{1}{2}, \frac{1}{2}} &=& \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{10} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{2,0,\frac{3}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{D(1232), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1232), \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{12}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{10} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{2,0,\frac{3}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{D(1600), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1600), \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{12}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{10} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} C^{\frac{1}{2},\lambda_{R}}_{2,0,\frac{3}{2},\lambda_{R}} \mathcal{H}^\mathrm{LS,production}_{D(1700), 2, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1700), \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{12}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{6} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{3}{2},\lambda_{R}} C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{D(1232), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1232), \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{12}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{6} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{3}{2},\lambda_{R}} C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{D(1600), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1600), \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{12}\right)}{2}} + \sum_{\lambda_{R}=-3/2}^{3/2}{\frac{\sqrt{6} \delta_{\frac{1}{2} \lambda_{R}} \mathcal{R}\left(\sigma_{3}\right) C^{\frac{1}{2},\lambda_{R}}_{1,0,\frac{3}{2},\lambda_{R}} C^{\frac{3}{2},\lambda_{R}}_{\frac{3}{2},\lambda_{R},0,0} \mathcal{H}^\mathrm{LS,production}_{D(1700), 1, \frac{3}{2}} \mathcal{H}^\mathrm{decay}_{D(1700), \frac{1}{2}, 0} d^{\frac{3}{2}}_{\lambda_{R},\frac{1}{2}}\left(\theta_{12}\right)}{2}} \\ \end{array}\end{split}\]

Show conversion factors for LHCb-PAPER-2022-002 Hide code cell source

H_prod = get_indexed_base("production", min_ls=False)

latex = R"""
\begin{array}{c|ccc|c}
  \textbf{Decay} & \textbf{coupling} & & & \textbf{factor} \\
  \hline
"""
for chain in LS_MODEL.decay.chains:
    R = Str(chain.resonance.name)
    L = chain.incoming_ls.L
    S = chain.incoming_ls.S
    symbol = H_prod[R, L, S]
    value = sp.sympify(LS_MODEL.parameter_defaults[symbol])
    factor = get_conversion_factor_ls(chain.resonance, L, S)
    coupling_value = f"{as_latex(symbol)} &=& {as_latex(value.n(3))}"
    latex += Rf"  {as_latex(chain)} & {coupling_value} & {factor:+d} \\" "\n"
latex += R"\end{array}"
Latex(f"{latex}")

Show conversion factors for LHCb-PAPER-2022-002 Hide code cell output

\[\begin{split}\begin{array}{c|ccc|c} \textbf{Decay} & \textbf{coupling} & & & \textbf{factor} \\ \hline \Lambda_c^+ \xrightarrow[S=1/2]{L=0} \Lambda(1405) \xrightarrow[S=1/2]{L=0} K^- p \pi^+ & \mathcal{H}^\mathrm{LS,production}_{L(1405), 0, \frac{1}{2}} &=& -1.22 - 0.0395 i & +1 \\ \Lambda_c^+ \xrightarrow[S=1/2]{L=1} \Lambda(1405) \xrightarrow[S=1/2]{L=0} K^- p \pi^+ & \mathcal{H}^\mathrm{LS,production}_{L(1405), 1, \frac{1}{2}} &=& 1.81 - 1.63 i & -1 \\ \Lambda_c^+ \xrightarrow[S=3/2]{L=1} \Lambda(1520) \xrightarrow[S=1/2]{L=2} K^- p \pi^+ & \mathcal{H}^\mathrm{LS,production}_{L(1520), 1, \frac{3}{2}} &=& 0.192 + 0.167 i & +1 \\ \Lambda_c^+ \xrightarrow[S=3/2]{L=2} \Lambda(1520) \xrightarrow[S=1/2]{L=2} K^- p \pi^+ & \mathcal{H}^\mathrm{LS,production}_{L(1520), 2, \frac{3}{2}} &=& -0.116 - 0.243 i & -1 \\ \Lambda_c^+ \xrightarrow[S=1/2]{L=0} \Lambda(1600) \xrightarrow[S=1/2]{L=1} K^- p \pi^+ & \mathcal{H}^\mathrm{LS,production}_{L(1600), 0, \frac{1}{2}} &=& 0.134 + 0.628 i & -1 \\ \Lambda_c^+ \xrightarrow[S=1/2]{L=1} \Lambda(1600) \xrightarrow[S=1/2]{L=1} K^- p \pi^+ & \mathcal{H}^\mathrm{LS,production}_{L(1600), 1, \frac{1}{2}} &=& 1.71 - 1.13 i & +1 \\ \Lambda_c^+ \xrightarrow[S=1/2]{L=0} \Lambda(1670) \xrightarrow[S=1/2]{L=0} K^- p \pi^+ & \mathcal{H}^\mathrm{LS,production}_{L(1670), 0, \frac{1}{2}} &=& 0.0092 - 0.201 i & +1 \\ \Lambda_c^+ \xrightarrow[S=1/2]{L=1} \Lambda(1670) \xrightarrow[S=1/2]{L=0} K^- p \pi^+ & \mathcal{H}^\mathrm{LS,production}_{L(1670), 1, \frac{1}{2}} &=& 0.115 + 0.168 i & -1 \\ \Lambda_c^+ \xrightarrow[S=3/2]{L=1} \Lambda(1690) \xrightarrow[S=1/2]{L=2} K^- p \pi^+ & \mathcal{H}^\mathrm{LS,production}_{L(1690), 1, \frac{3}{2}} &=& -0.379 + 0.331 i & +1 \\ \Lambda_c^+ \xrightarrow[S=3/2]{L=2} \Lambda(1690) \xrightarrow[S=1/2]{L=2} K^- p \pi^+ & \mathcal{H}^\mathrm{LS,production}_{L(1690), 2, \frac{3}{2}} &=& 0.286 - 0.248 i & -1 \\ \Lambda_c^+ \xrightarrow[S=1/2]{L=0} \Lambda(2000) \xrightarrow[S=1/2]{L=0} K^- p \pi^+ & \mathcal{H}^\mathrm{LS,production}_{L(2000), 0, \frac{1}{2}} &=& 2.81 + 0.0715 i & +1 \\ \Lambda_c^+ \xrightarrow[S=1/2]{L=1} \Lambda(2000) \xrightarrow[S=1/2]{L=0} K^- p \pi^+ & \mathcal{H}^\mathrm{LS,production}_{L(2000), 1, \frac{1}{2}} &=& 0.891 + 0.0874 i & -1 \\ \Lambda_c^+ \xrightarrow[S=3/2]{L=1} \Delta(1232) \xrightarrow[S=1/2]{L=1} p \pi^+ K^- & \mathcal{H}^\mathrm{LS,production}_{D(1232), 1, \frac{3}{2}} &=& -1.5 + 3.16 i & +1 \\ \Lambda_c^+ \xrightarrow[S=3/2]{L=2} \Delta(1232) \xrightarrow[S=1/2]{L=1} p \pi^+ K^- & \mathcal{H}^\mathrm{LS,production}_{D(1232), 2, \frac{3}{2}} &=& 0.587 - 0.839 i & -1 \\ \Lambda_c^+ \xrightarrow[S=3/2]{L=1} \Delta(1600) \xrightarrow[S=1/2]{L=1} p \pi^+ K^- & \mathcal{H}^\mathrm{LS,production}_{D(1600), 1, \frac{3}{2}} &=& 1.6 - 2.46 i & +1 \\ \Lambda_c^+ \xrightarrow[S=3/2]{L=2} \Delta(1600) \xrightarrow[S=1/2]{L=1} p \pi^+ K^- & \mathcal{H}^\mathrm{LS,production}_{D(1600), 2, \frac{3}{2}} &=& 0.432 - 0.689 i & -1 \\ \Lambda_c^+ \xrightarrow[S=3/2]{L=1} \Delta(1700) \xrightarrow[S=1/2]{L=2} p \pi^+ K^- & \mathcal{H}^\mathrm{LS,production}_{D(1700), 1, \frac{3}{2}} &=& -3.16 + 2.29 i & -1 \\ \Lambda_c^+ \xrightarrow[S=3/2]{L=2} \Delta(1700) \xrightarrow[S=1/2]{L=2} p \pi^+ K^- & \mathcal{H}^\mathrm{LS,production}_{D(1700), 2, \frac{3}{2}} &=& 0.179 - 0.299 i & +1 \\ \Lambda_c^+ \xrightarrow[S=1/2]{L=0} K(700) \xrightarrow[S=0]{L=0} \pi^+ K^- p & \mathcal{H}^\mathrm{LS,production}_{K(700), 0, \frac{1}{2}} &=& -0.000167 - 0.685 i & +1 \\ \Lambda_c^+ \xrightarrow[S=1/2]{L=1} K(700) \xrightarrow[S=0]{L=0} \pi^+ K^- p & \mathcal{H}^\mathrm{LS,production}_{K(700), 1, \frac{1}{2}} &=& -0.631 + 0.0404 i & +1 \\ \Lambda_c^+ \xrightarrow[S=1/2]{L=0} K(892) \xrightarrow[S=0]{L=1} \pi^+ K^- p & \mathcal{H}^\mathrm{LS,production}_{K(892), 0, \frac{1}{2}} &=& 1.0 & +1 \\ \Lambda_c^+ \xrightarrow[S=1/2]{L=1} K(892) \xrightarrow[S=0]{L=1} \pi^+ K^- p & \mathcal{H}^\mathrm{LS,production}_{K(892), 1, \frac{1}{2}} &=& -0.342 + 0.064 i & -1 \\ \Lambda_c^+ \xrightarrow[S=3/2]{L=1} K(892) \xrightarrow[S=0]{L=1} \pi^+ K^- p & \mathcal{H}^\mathrm{LS,production}_{K(892), 1, \frac{3}{2}} &=& -0.755 - 0.592 i & +1 \\ \Lambda_c^+ \xrightarrow[S=3/2]{L=2} K(892) \xrightarrow[S=0]{L=1} \pi^+ K^- p & \mathcal{H}^\mathrm{LS,production}_{K(892), 2, \frac{3}{2}} &=& -0.0938 - 0.38 i & -1 \\ \Lambda_c^+ \xrightarrow[S=1/2]{L=0} K(1430) \xrightarrow[S=0]{L=0} \pi^+ K^- p & \mathcal{H}^\mathrm{LS,production}_{K(1430), 0, \frac{1}{2}} &=& -1.35 - 3.15 i & +1 \\ \Lambda_c^+ \xrightarrow[S=1/2]{L=1} K(1430) \xrightarrow[S=0]{L=0} \pi^+ K^- p & \mathcal{H}^\mathrm{LS,production}_{K(1430), 1, \frac{1}{2}} &=& 0.598 - 0.956 i & +1 \\ \end{array}\end{split}\]

It is asserted that these amplitude expressions to not evaluate to \(0\) once the Clebsch-Gordan coefficients are evaluated.

Show code cell content Hide code cell content

def assert_non_zero_amplitudes(model: AmplitudeModel) -> None:
    for amplitude in tqdm(model.amplitudes.values(), disable=NO_TQDM):
        assert amplitude.doit() != 0


assert_non_zero_amplitudes(LS_MODEL)

See also

See Resonances and LS-scheme for the allowed \(LS\)-values.

7.7.2. Distribution

Convert expressions to numerical functions Hide code cell content

def lambdify(model: AmplitudeModel) -> sp.Expr:
    intensity_expr = unfold_intensity(model)
    pars = model.parameter_defaults
    free_parameters = {s: v for s, v in pars.items() if "production" in str(s)}
    fixed_parameters = {s: v for s, v in pars.items() if s not in free_parameters}
    subs_intensity_expr = intensity_expr.xreplace(fixed_parameters)
    return perform_cached_lambdify(subs_intensity_expr, free_parameters)


def unfold_intensity(model: AmplitudeModel) -> sp.Expr:
    unfolded_intensity = perform_cached_doit(model.intensity)
    return perform_cached_doit(unfolded_intensity.xreplace(model.amplitudes))


NOMINAL_MODEL = formulate_model("Default amplitude model")
NOMINAL_INTENSITY_FUNC = lambdify(NOMINAL_MODEL)
LS_INTENSITY_FUNC = lambdify(LS_MODEL)

Create phase space grid Hide code cell content

GRID = generate_meshgrid_sample(NOMINAL_MODEL.decay, resolution=300)
TRANSFORMER = create_data_transformer(NOMINAL_MODEL)
GRID.update(TRANSFORMER(GRID))

Show code cell source Hide code cell source

def compare_2d_distributions() -> None:
    NOMINAL_INTENSITIES = compute_normalized_intensity(NOMINAL_INTENSITY_FUNC)
    LS_INTENSITIES = compute_normalized_intensity(LS_INTENSITY_FUNC)
    max_intensity = max(
        jnp.nanmax(NOMINAL_INTENSITIES),
        jnp.nanmax(LS_INTENSITIES),
    )
    use_mpl_latex_fonts()
    fig, axes = plt.subplots(
        dpi=200,
        figsize=(12, 5),
        ncols=2,
    )
    for ax in axes:
        ax.set_box_aspect(1)
    ax1, ax2 = axes
    ax1.set_title("Nominal model")
    ax2.set_title("LS-model")
    ax1.pcolormesh(
        GRID["sigma1"],
        GRID["sigma2"],
        NOMINAL_INTENSITIES,
        vmax=max_intensity,
    )
    ax2.pcolormesh(
        GRID["sigma1"],
        GRID["sigma2"],
        LS_INTENSITIES,
        vmax=max_intensity,
    )
    plt.show()


def compute_normalized_intensity(func: Function) -> jax.Array:
    intensities = func(GRID)
    integral = jnp.nansum(intensities)
    return intensities / integral


compare_2d_distributions()

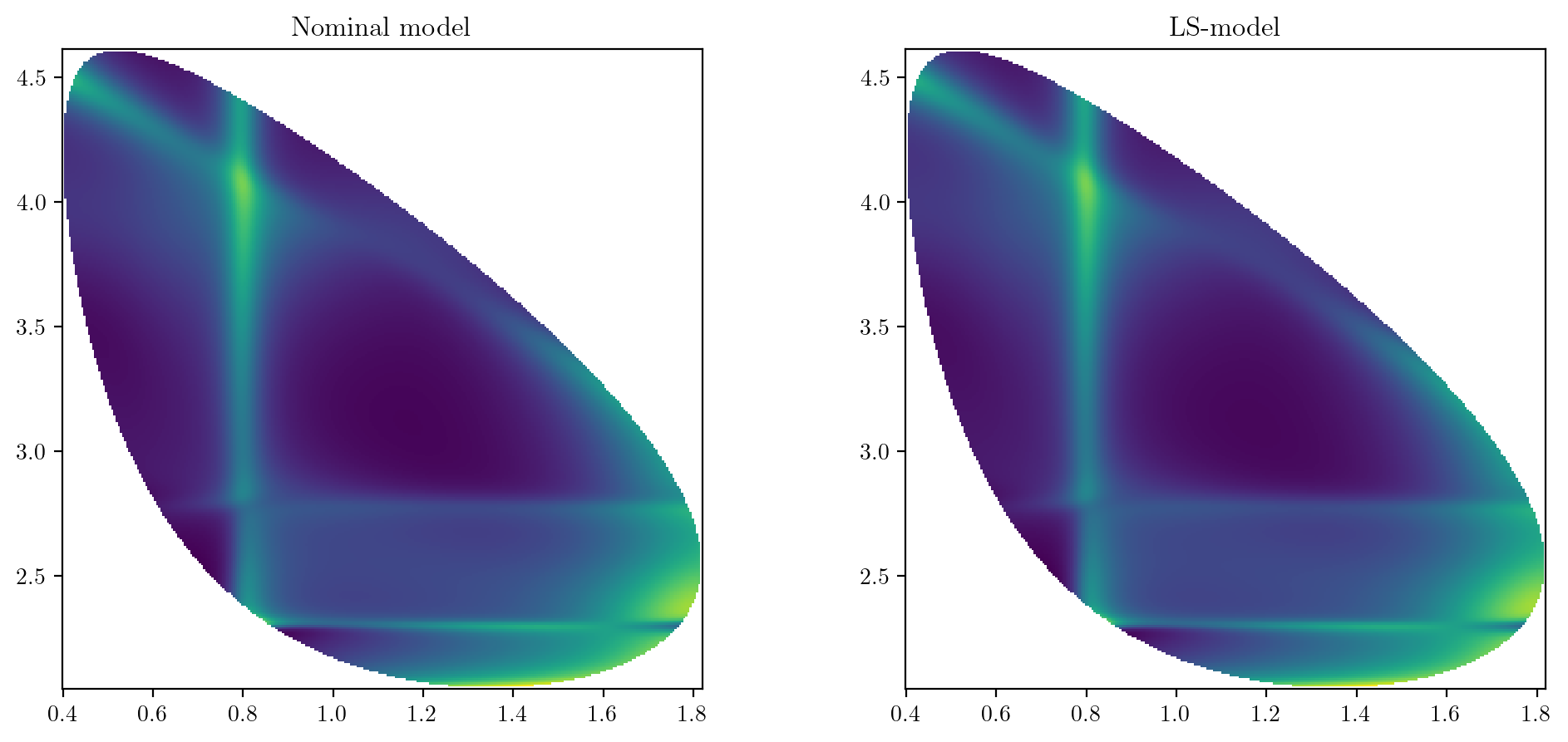
7.7.3. Decay rates

Show code cell source Hide code cell source

def to_regex(text: str) -> str:
    text = text.replace("(", r"\(")
    return text.replace(")", r"\)")


def compute_decay_rates() -> dict[Particle, tuple[float, float]]:
    decay_rates = {}
    nominal_I_tot = integrate_intensity(NOMINAL_INTENSITY_FUNC(PHSP))
    LS_I_tot = integrate_intensity(LS_INTENSITY_FUNC(PHSP))
    for chain in tqdm(NOMINAL_MODEL.decay.chains, disable=NO_TQDM):
        filter_ = [to_regex(chain.resonance.name)]
        LS_I_sub = sub_intensity(LS_INTENSITY_FUNC, PHSP, filter_)
        nominal_I_sub = sub_intensity(NOMINAL_INTENSITY_FUNC, PHSP, filter_)
        decay_rates[chain.resonance] = (
            float(nominal_I_sub / nominal_I_tot),
            float(LS_I_sub / LS_I_tot),
        )
    return decay_rates


PHSP = generate_phasespace_sample(NOMINAL_MODEL.decay, n_events=100_000, seed=0)
PHSP = TRANSFORMER(PHSP)
DECAY_RATES = compute_decay_rates()
src = R"""
\begin{array}{l|rr|r}
  \textbf{Resonance} & \textbf{Nominal} & \textbf{LS-model} & \textbf{Difference}\\
  \hline
"""
for res, (nominal_rate, ls_rate) in DECAY_RATES.items():
    nominal_rate *= 100
    ls_rate *= 100
    src += (
        Rf"  {res.latex} & {nominal_rate:.2f} & {ls_rate:.2f} &"
        rf" {ls_rate - nominal_rate:+.2f} \\"
        "\n"
    )
    del res, nominal_rate, ls_rate
src += R"\end{array}"
Latex(src)

\[\begin{split}\begin{array}{l|rr|r} \textbf{Resonance} & \textbf{Nominal} & \textbf{LS-model} & \textbf{Difference}\\ \hline \Lambda(1405) & 7.78 & 7.02 & -0.75 \\ \Lambda(1520) & 1.91 & 1.95 & +0.03 \\ \Lambda(1600) & 5.16 & 5.21 & +0.05 \\ \Lambda(1670) & 1.15 & 1.18 & +0.02 \\ \Lambda(1690) & 1.16 & 1.09 & -0.08 \\ \Lambda(2000) & 9.55 & 9.84 & +0.30 \\ \Delta(1232) & 28.73 & 28.97 & +0.24 \\ \Delta(1600) & 4.50 & 4.24 & -0.26 \\ \Delta(1700) & 3.89 & 3.99 & +0.10 \\ K(700) & 2.99 & 3.25 & +0.26 \\ K(892) & 21.95 & 21.25 & -0.70 \\ K(1430) & 14.70 & 15.41 & +0.71 \\ \end{array}\end{split}\]

Tip

Compare with the values with uncertainties as reported in Decay rates.